MATERI MATEMATIKA KELAS 8 SMP/MTSn BAB 1 : Faktorisasi Suku Aljabar
FAKTORISASI SUKU ALJABAR
RINGKASAN MATERI
A. Pengertian Faktorisasi
Faktorisasi aljabar adalah mengubah penjumlahan aljabar menjadi perkalian faktor-faktornya.
Contoh :
Karena 8 = 1 x 8, atau 8 = 2 x 4, maka 1, 2, 4 dan 8 adalah faktor-faktor dari 8
B. Bentuk Distributif
ab + ac = a(b + c)
ab – ac = a(b – c), dengan a adalah faktor suku aljabar yang sama.
Contoh :
15p2 + 9p = 3p(5p + 3)
C. Bentuk Selisih Dua Kuadrat
a2 – b2 = (a + b)(a – b)
Contoh :
16m2 – 9 = (4m + 3)(4m – 3)
D. Bentuk Kuadrat Sempurna
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
Contoh :
x2 + 10x + 25 = (x + 5)2
x2 – 16x + 64 = (x – 8)2
E. Bentuk ax2 + bx +c, dengan a = 1
x2 + bx + c = (x + p)(x + q)
dengan syarat : pq = c dan p + q = b
Contoh :
x2 + 8x + 12 =(x + 2)(x + 6)
F. Bentuk ax2 + bx +c, dengan a ≠ 1
G. Menyederhanakan Pecahan Aljabar
Contoh :
Cara : Bentuk aljabar difaktorkan dan faktor yang sama di hilangkan
FAKTORISASI SUKU ALJABAR
RINGKASAN MATERI
A. Pengertian Faktorisasi
Faktorisasi aljabar adalah mengubah penjumlahan aljabar menjadi perkalian faktor-faktornya.
Contoh :
Karena 8 = 1 x 8, atau 8 = 2 x 4, maka 1, 2, 4 dan 8 adalah faktor-faktor dari 8
B. Bentuk Distributif
ab + ac = a(b + c)
ab – ac = a(b – c), dengan a adalah faktor suku aljabar yang sama.
Contoh :
15p2 + 9p = 3p(5p + 3)
C. Bentuk Selisih Dua Kuadrat
a2 – b2 = (a + b)(a – b)
Contoh :
16m2 – 9 = (4m + 3)(4m – 3)
D. Bentuk Kuadrat Sempurna
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
Contoh :
x2 + 10x + 25 = (x + 5)2
x2 – 16x + 64 = (x – 8)2
E. Bentuk ax2 + bx +c, dengan a = 1
x2 + bx + c = (x + p)(x + q)
dengan syarat : pq = c dan p + q = b
Contoh :
x2 + 8x + 12 =(x + 2)(x + 6)
F. Bentuk ax2 + bx +c, dengan a ≠ 1
G. Menyederhanakan Pecahan Aljabar
Contoh :
Cara : Bentuk aljabar difaktorkan dan faktor yang sama di hilangkanMATERI MATEMATIKA KELAS 8 SMP/MTSn BAB 2 : Relasi dan Fungsi
Relasi
Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.
Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.
Definisi
Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari A keB adalah subhimpunan dari A×B.
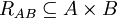
Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari A keB adalah subhimpunan dari A×B.
Relasi dan fungsi proposisi
Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunanW = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R = {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisiw(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.
Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunanW = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R = {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisiw(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunanW = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R = {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisiw(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.
Relasi A×A
Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:
- Refleksif
- Irefleksif
- Simetrik
- Anti-simetrik
- Transitif
Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.
Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:
- Refleksif
- Irefleksif
- Simetrik
- Anti-simetrik
- Transitif
Relasi Refleksif
Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dirinya sendiri.

atau

Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan xdan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.
Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dirinya sendiri.
Relasi Irefleksif
Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.

atau

Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
Relasi Simetrik
Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota Aberhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.

atau

Sebuah relasi “x + y genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota Aberhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.
Relasi Anti-simetrik
Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi adan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.

atau

Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.

atau

Relasi  bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku 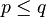 dan
dan 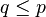 berarti p = q.
berarti p = q.
Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi adan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.
 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku 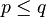 dan
dan 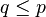 berarti p = q.
berarti p = q.
 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku 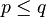 dan
dan 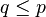 berarti p = q.
berarti p = q.Relasi Transitif
Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan bberhubungan dengan c, maka a berhubungan dengan c secara langsung.

atau

Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7.
Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan bberhubungan dengan c, maka a berhubungan dengan c secara langsung.
Relasi khusus
Relasi Ekivalen
Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:
- Refleksif
- Simetrik, dan
- Transitif
Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.
Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:
- Refleksif
- Simetrik, dan
- Transitif
Orde Parsial
Orde parsial adalah relasi yang bersifat:
- Refleksif
- Anti-simetrik, dan
- Transitif
Orde parsial adalah relasi yang bersifat:
- Refleksif
- Anti-simetrik, dan
- Transitif
Fungsi (matematika)
Fungsi, dalam istilah matematika adalah pemetaan setiap anggota sebuah himpunan(dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagaikodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10
Fungsi, dalam istilah matematika adalah pemetaan setiap anggota sebuah himpunan(dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagaikodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10
Notasi
Untuk mendefinisikan fungsi dapat digunakan notasi berikut.

Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.


atau
Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
Fungsi sebagai relasi
Sebuah fungsi f dapat dimengerti sebagai relasi antara dua himpunan, dengan unsur pertama hanya dipakai sekali dalam relasi tersebut.
Sebuah fungsi f dapat dimengerti sebagai relasi antara dua himpunan, dengan unsur pertama hanya dipakai sekali dalam relasi tersebut.
Domain dan Kodomain
Domain adalah daerah asal, kodomain adalah daerah kawan, sedangkan range adalah daerah hasil
Domain adalah daerah asal, kodomain adalah daerah kawan, sedangkan range adalah daerah hasil
Jenis-jenis fungsi
Fungsi injektif
Fungsi f: A → B disebut fungsi satu-satu atau fungsi injektif jika dan hanya jika untuk sebarang a1 dan a2 dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
Fungsi f: A → B disebut fungsi satu-satu atau fungsi injektif jika dan hanya jika untuk sebarang a1 dan a2 dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
 dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).
dengan a1 tidak sama dengan a2berlaku f(a1) tidak sama dengan f(a2). Dengan kata lain, bila a1 = a2 maka f(a1) sama dengan f(a2).Fungsi surjektif
Fungsi f: A → B disebut fungsi kepadaatau fungsi surjektif jika dan hanya jika untuk sebarang b dalam kodomain Bterdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range).
Fungsi f: A → B disebut fungsi kepadaatau fungsi surjektif jika dan hanya jika untuk sebarang b dalam kodomain Bterdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range).
Fungsi bijektif
Fungsi f: A → B disebut disebut fungsi bijektif jika dan hanya jika untuk sebarang b dalam kodomain B terdapat tepat satu a dalam domain A sehinggaf(a) = b, dan tidak ada anggota A yang tidak terpetakan dalam B. Dengan kata lain, fungsi bijektif adalah sekaligus injektif dan surjektif.

Fungsi f: A → B disebut disebut fungsi bijektif jika dan hanya jika untuk sebarang b dalam kodomain B terdapat tepat satu a dalam domain A sehinggaf(a) = b, dan tidak ada anggota A yang tidak terpetakan dalam B. Dengan kata lain, fungsi bijektif adalah sekaligus injektif dan surjektif.
MATERI MATEMATIKA KELAS 8 SMP/MTSn BAB 3 : Persamaan Garis Lurus
1. Definisi Gradien
Gradien suatu garis lurus adalah : Perbandingan antara komponen y (ordinat) dan komponen x(absis) antara dua titik pada garis itu. Gradien suatu garis biasanya dinotasikan dengan huruf kecilm. Perhatikan gambar di bawah ini !
komponen y dari garis AB = y2 - y1 ; komponen x dari garis AB = x2 - x1, maka :

 Catatan : gradien sebuah garis sering disebut kecondongan sebuah garis atau koefisien arahsebuah garis.
Catatan : gradien sebuah garis sering disebut kecondongan sebuah garis atau koefisien arahsebuah garis.
1.1. Macam-macam gradien
a. Gradien bernilai positif
 Garis l condong ke kanan , maka ml bernilai positif
b. Gradien bernilai negatif
Garis l condong ke kanan , maka ml bernilai positif
b. Gradien bernilai negatif
 Garis k condong ke kiri , maka mk bernilai negatif
Garis k condong ke kiri , maka mk bernilai negatif
Gradien dari sebuah persamaan garis
Jika sebuah garis mempunyai persamaan ax + by = c, maka gradien persamaan garis itu ialah : 
c. Gradien garis melalui pangkal koordinat
 Garis l melalui pangkal koordinat (0,0) maka
Garis l melalui pangkal koordinat (0,0) maka  d. Gradien dua garis yang sejajar
d. Gradien dua garis yang sejajar
 Dua garis yang sejajar mempunyai gradien yang sama, garis l dan garis k sejajar, maka ml = mk
e. Gradien dua garis yang saling tegak lurus
Dua garis yang sejajar mempunyai gradien yang sama, garis l dan garis k sejajar, maka ml = mk
e. Gradien dua garis yang saling tegak lurus
 Dua garis yang saling tegak lurus perkalian gradiennya adalah -1.Garis l dan garis k saling tegak lurus, maka ml x mk = -1.
Dua garis yang saling tegak lurus perkalian gradiennya adalah -1.Garis l dan garis k saling tegak lurus, maka ml x mk = -1.
1.2. Contoh-Contoh Soal
Contoh 1 :
Tentukanlah gradien garis :
-
melalui titik P(2,-5) dan titik Q(-9,3)
-
melalui pangkal koordinat dan titik A(-2,-8)
Penyelesaian :
a. Melalui titik P(2,-5) dan titik Q(-9,3)
P(2,-5) berarti x1 = 2 , y1 = -5
Q(-9,3) berarti x2 = -9 , y2 = 3




 Jadi gradient melalui titik P(2,-5) dan titik Q(-9,3) adalah
Jadi gradient melalui titik P(2,-5) dan titik Q(-9,3) adalah 
b. Melalui pangkal koordinat dan titik A(-2,-8)
A(-2,-8) berarti x = -2 , y1 = -8


 Jadi gradient melalui pangkal koordinat dan titik A(-2,-8) adalah 4
Jadi gradient melalui pangkal koordinat dan titik A(-2,-8) adalah 4
Contoh 2 :
Tentukanlah gradient sebuah garis :
-
yang sejajar dengan garis 4x + 2y = 6
-
yang tegak lurus dengan garis x - 4y = 10
Penyelesaian :
-
Persamaan garis 4x + 2y = 6, maka a = 4, b = 2
 Dua garis yang sejajar : m1 = m2 , maka m2 = - 2
Dua garis yang sejajar : m1 = m2 , maka m2 = - 2
-
Persamaan garis x - 4y = 10, maka a = 1, b = -4
 Dua garis yang tegak lurus : m1 x m2 = -1 , maka
Dua garis yang tegak lurus : m1 x m2 = -1 , maka 

(Sumber:Hipupsmart27.blogspot.com)
1. Definisi Gradien



 Garis k condong ke kiri , maka mk bernilai negatif
Garis k condong ke kiri , maka mk bernilai negatif














Gradien suatu garis lurus adalah : Perbandingan antara komponen y (ordinat) dan komponen x(absis) antara dua titik pada garis itu. Gradien suatu garis biasanya dinotasikan dengan huruf kecilm. Perhatikan gambar di bawah ini !
komponen y dari garis AB = y2 - y1 ; komponen x dari garis AB = x2 - x1, maka :
Catatan : gradien sebuah garis sering disebut kecondongan sebuah garis atau koefisien arahsebuah garis.
1.1. Macam-macam gradien
a. Gradien bernilai positif

Garis l condong ke kanan , maka ml bernilai positif
b. Gradien bernilai negatif

Gradien dari sebuah persamaan garis
Jika sebuah garis mempunyai persamaan ax + by = c, maka gradien persamaan garis itu ialah : 
c. Gradien garis melalui pangkal koordinat

Garis l melalui pangkal koordinat (0,0) maka 
d. Gradien dua garis yang sejajar

Dua garis yang sejajar mempunyai gradien yang sama, garis l dan garis k sejajar, maka ml = mk
e. Gradien dua garis yang saling tegak lurus

Dua garis yang saling tegak lurus perkalian gradiennya adalah -1.Garis l dan garis k saling tegak lurus, maka ml x mk = -1.
1.2. Contoh-Contoh Soal
Contoh 1 :
Tentukanlah gradien garis :
- melalui titik P(2,-5) dan titik Q(-9,3)
- melalui pangkal koordinat dan titik A(-2,-8)
Penyelesaian :
a. Melalui titik P(2,-5) dan titik Q(-9,3)
P(2,-5) berarti x1 = 2 , y1 = -5
Q(-9,3) berarti x2 = -9 , y2 = 3
Jadi gradient melalui titik P(2,-5) dan titik Q(-9,3) adalah 
b. Melalui pangkal koordinat dan titik A(-2,-8)
A(-2,-8) berarti x = -2 , y1 = -8
Jadi gradient melalui pangkal koordinat dan titik A(-2,-8) adalah 4
Contoh 2 :
Tentukanlah gradient sebuah garis :
- yang sejajar dengan garis 4x + 2y = 6
- yang tegak lurus dengan garis x - 4y = 10
Penyelesaian :
- Persamaan garis 4x + 2y = 6, maka a = 4, b = 2
Dua garis yang sejajar : m1 = m2 , maka m2 = - 2
- Persamaan garis x - 4y = 10, maka a = 1, b = -4
Dua garis yang tegak lurus : m1 x m2 = -1 , maka 
(Sumber:Hipupsmart27.blogspot.com)



Tidak ada komentar :
Posting Komentar